Az új koronavírus (SARS-CoV-2) hazánkban is megjelent és jelentős figyelmet vált ki a lakosság és a szakemberek körében is. A kutatók elsősorban az új-koronavírus-betegség (COVID-19) megfékezésének lehetőségeivel foglalkoznak, a vírus biológiáját, humán hatásait és terjedését vizsgálják.
Az idősebb emberekre jelentősen veszélyesebb a fertőzés. A nagyobb betegségteherrel élők is veszélyeztetettebbek (transzplantáltak, immunszupresszáltak, egyes súlyos krónikus betegségben szenvedők stb.).
Minden jelentősebb tudományos kiadó online gyűjteményeket hozott létre, ahol a vonatkozó közleményeket és adatokat ingyenesen elérhetővé tették (pl.: Lancet , Elsevier , NEJM stb.). Páratlan nemzetközi tudományos együttműködés látszik kialakulni a vírus terjedésének megfékezésére.
A társadalomtudomány is érintett a kérdésben. A vírus terjedésére a társadalmi viselkedés is hatással van; a terjedést befolyásolják az adott ország közlekedési rendszerének sajátosságai, az ingázás, a népsűrűség, a korfa, a zsúfoltság, a településszerkezet, az érintkezési szokások, a háztartások összetétele, az általános higiéné, az egészségviselkedés, az egészségügyi ellátórendszer infrastruktúrája, a kormányzati intézkedések, a bizalom, a normakövetés és még számos más paraméter. Számít a különböző országokkal való közlekedési kapcsolat is, a terjedés kezdeti szakaszában például a légi közlekedés különösen fontos tényező.
Vezető járványügyi szakemberek korszerű modellezés segítségével április elejére becsülték a járvány csúcsát Kínában, amennyiben sem közlekedési, sem fertőzés-transzmissziós szempontból nem történik változás. Jelenleg úgy tűnik, hogy nagy erőfeszítésekkel sikerült Kínában megfékezni az új fertőzések számának emelkedését. Az új adatok beérkezésével számos a vírus terjedésében szerepet játszó paraméter tisztul, pontosabbá válik. Magyar szakemberek pedig egy fejlett módszertant használva jó becslést tudtak adni a Kínán kívüli fertőzésterjedés kockázatára, és javaslatokat is tettek a kockázat csökkentésére.
Magyarországra vonatkozóan a járvány terjedésére irányuló professzionális becslést nem találtam, ezért társadalomtudományi egyetemi hallgatóként egy egyszerű, naiv becslést készítettem online elérhető adatokból. A modern (sztochasztikus, hálózatos, változó paraméterű) járványterjedési modellek tükrében az én itt ismertetett modellem meghaladott, nem számít professzionális becslésnek.
A Johns Hopkins Egyetem által nyilvánosan közzétett adatokból leválogattam azon európai országok adatait, amelyekben 2020. január 30. óta jelen van a fertőzés.
A vizsgált nyolc európai országban eltérő módon alakult a fertőzöttek számának növekedése. Az y tengely az igazolt betegek száma (logaritmikus), az x pedig a napok száma.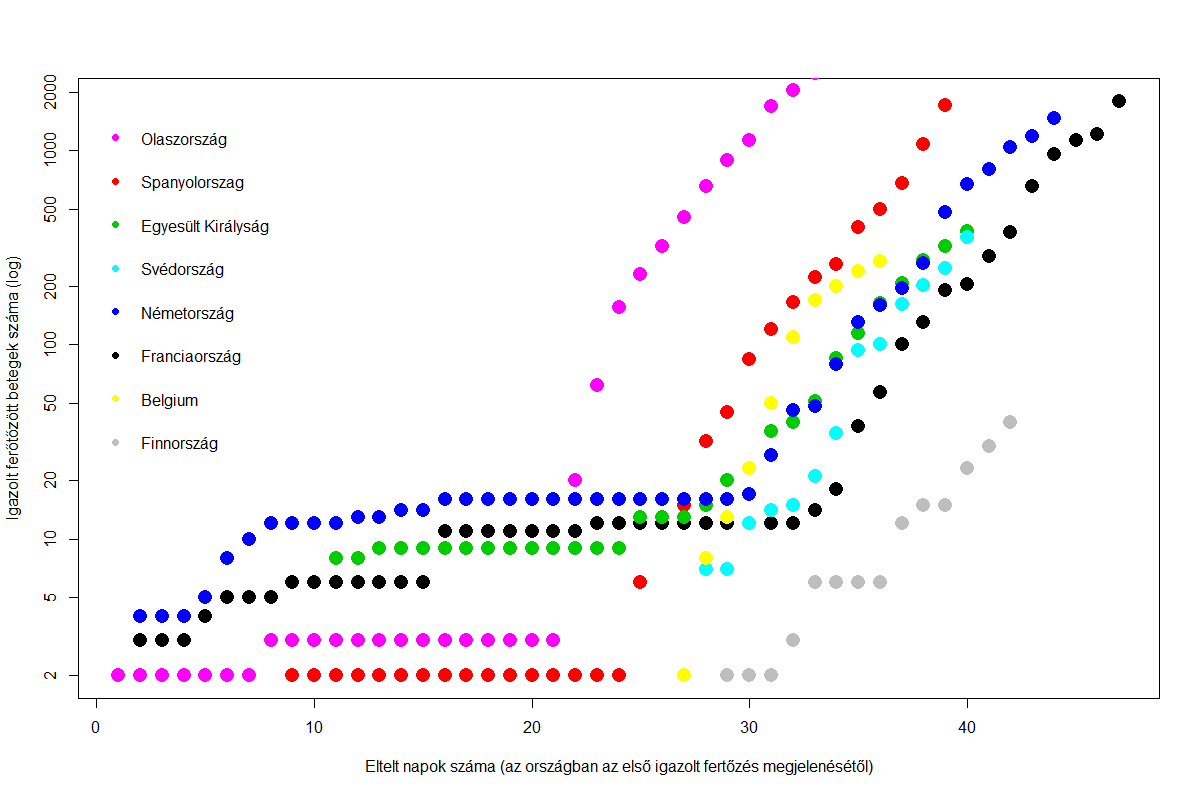
A fenti ábrán jól látható, hogy körülbelül 17 fertőzött felett mind a nyolc országban megugrott a fertőzöttek számának emelkedése, ezért a 17 feletti szakaszokra a fertőzöttek lakosságarányos értékeire exponenciális függvényeket illesztettem. (Az exponenciális függvény ugyanakkor csak a terjedés kezdeti időszakára ad jó becslést, később a logaritmikus függvény illeszthető jobban. A "nyers emelkedés" mögött pedig egy alapvetően hálózatos elemzéssel modellezhető jelenség áll.)
A vizsgált nyolc európai országban a népsűrűség, a nagy (évi egymillió főnél több utast szállító) repterek száma, az egy háztartásban élők átlagos értéke, és járvány 17 fertőzött feletti (lakosságarányos) felfutására illesztett exponenciális függvény fontosabb paraméterei (C a konstans, ahol a függvény az y tengely metszi; a béta az e kitevőjében szereplő szorzó)
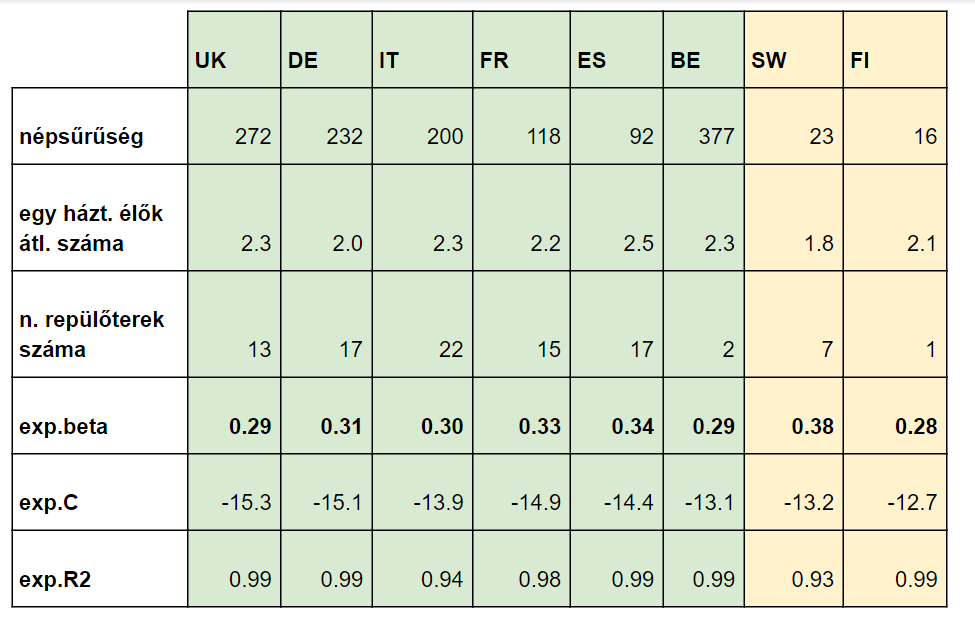
Amennyiben a járvány kezdeti szakaszát (a 17 fertőzött alatti értékeket) is figyelembe vettem, akkor – a szakirodalommal összhangban – a nagy nemzetközi repülőterek száma (egyszerű kétváltozós lineáris modellben) bírt befolyással (p=0.0445, R négyzet=0,7) az exponenciális emelkedés kitevőjére. Ám a 17 feletti szakaszra vizsgálva már elvesztette befolyásoló erejét (p=0.668). A népsűrűség és az egy háztartásban élők átlagos száma szintén nem volt befolyásoló tényező (a kitevőre) ebben a modellben.
A magyar adatok még nem elégségesek ahhoz, hogy ilyen jellegű illesztést lehessen tenni, hiszen hazánkban még nincs 17 igazoltan fertőzött beteg, ezért az exponenciális paramétereket ezen nyolc ország adataiból becsültem. A konstans (C) és béta paraméterek is Shapiro-Wilk teszttel normálisnak bizonyultak (bár egyes statisztikusok szerint paraméterek normalitását nem szabad vizsgálni) (W = 0.9, p = 0.4), ezért egyszerű t-becslőfüggvényt használtam. Ezen előzetes, naiv modell alapján a (lakosságarányos) exponenciális függvény becsült paraméterei a következők lettek C= -14.0 [95% CI (-14.8) - (-13.4) ], beta=0.31 [95% CI 0.29 - 0.34]. Ebben a tartományban gyakorlatilag csak Finnország (0.28) és Svédország(0.38) nincs benne.
Ezen paraméterekkel becsülve a hazai exponenciális növekedést, adaptálva a lakosságszámra és az ismert betegszámra, valamint az illesztés önálló bizonytalanságát is bekalkulálva, ez a kezdetleges modell a 17. igazolt beteg megjelenése utáni 14. napon 1161 [90% CI 374 - 3599] fertőzöttet jósol. (Ha semmilyen kormányzati intézkedés nem történik, és az egyéb paraméterek is változatlanok maradnak, illetve Magyarországon is hasonló módon történik a felfutás, mint a vizsgált nyolc országban és az alap szaporodási ráta is változatlan.)
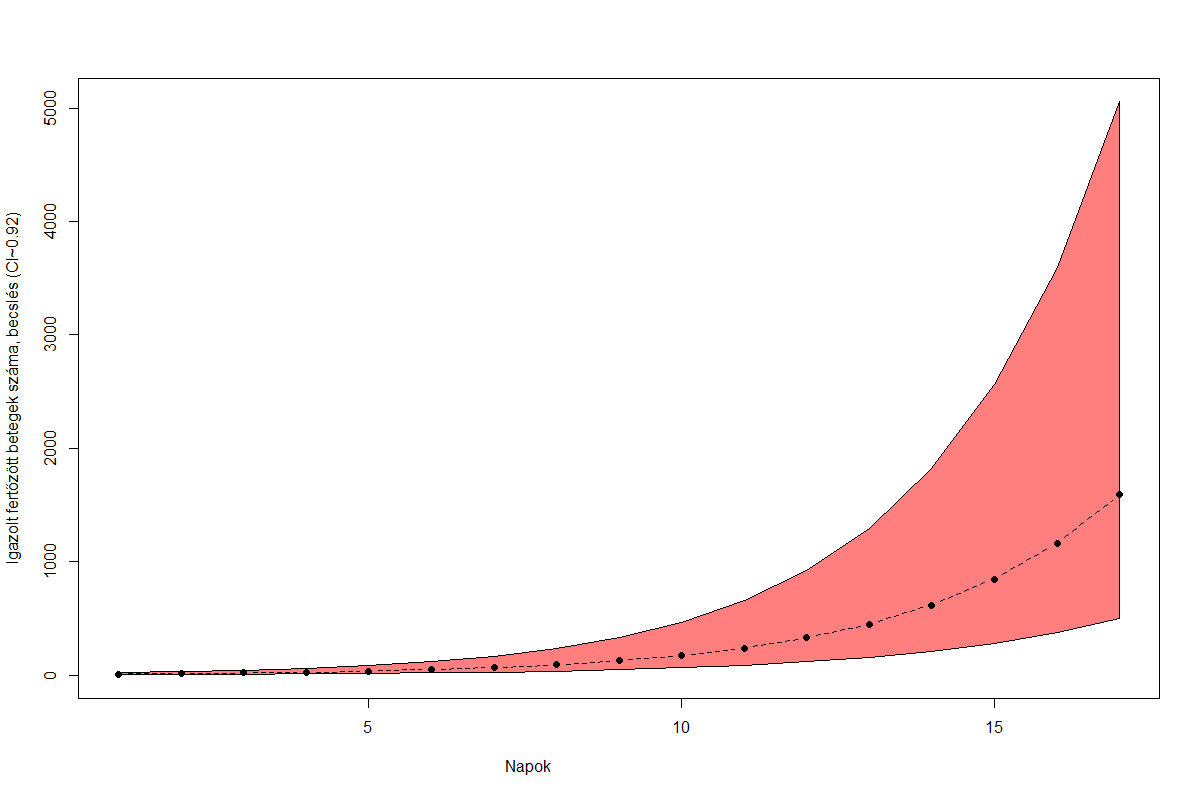
A 17. fertőzött megjelenése utáni felfutás magyar adatokra adaptálva, naiv exponenciális modellben, beavatkozások nélkül
Hosszabb távú becslésre ezen módszer nem alkalmas, mert a járvány terjedése csak kezdetileg exponenciális, ezért ezen becsült adatsort a leges-legegyszerűbb fertőzési modellbe (a SIR modellbe) illesztettem. A SIR szemlélet a populációt három csoportra osztja a fertőzés szempontjából: fertőzhető, fertőzött, gyógyult. A három közötti kapcsolatot pedig egyszerű differenciálegyenletekkel határozza meg. Az alapvető SIR modellbe ezen becsült 14 napos felfutási adatokat megadva, Magyarország lakosságára adaptálva 44 [39 - 50] eltelt napra számolta ki a járvány csúcsát. (SIR-beta: 0.65+-0.01, SIR-gamma: 0.34+-0.01). A modellnek erős korlátai vannak: becsült adatokat használtam, valamint a SIR determinisztikus, nem számol a paraméterek változásával, valamint a fertőzés hálózatos jellegével sem, és a fertőzés megakadályozására tett intézkedéseket sem veszi figyelembe. (A járvány lassítása fontos teendő.)
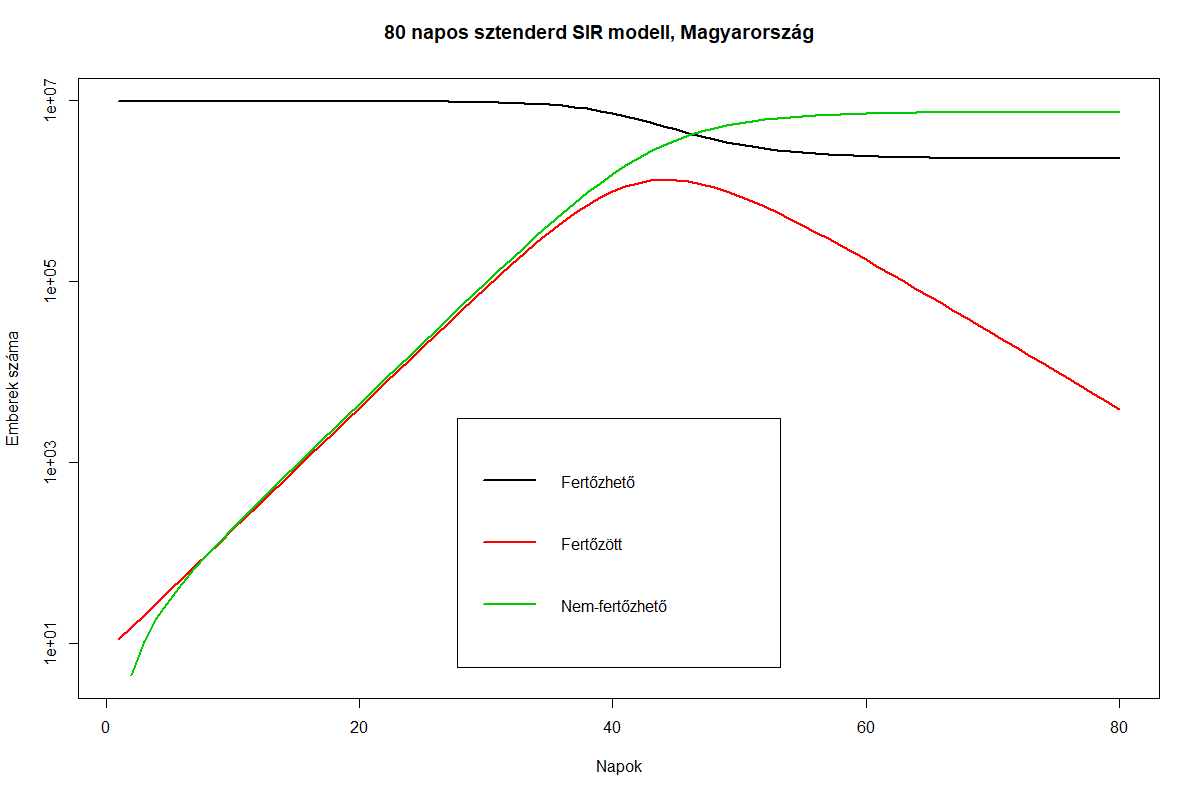
A 17. fertőzött megjelenése utáni 14 nap becsült értékeinek a sztenderd SIR modellben 80 napra szimulálva (béta=0,65, gamma=0.34) magyar lakossági adatokon, hatósági beavatkozások nélkül
A bemutatott naiv becslésnél modernebb, járványtanilag korrektebb, több magyarázó változót használó, sztochasztikus, változó paraméterterű, és hálózatos adatokat is kezelő modellek készíthetőek, ezekkel pontosabb és megbízhatóbb becslések készíthetőek, ám ez már járványterjedéssel foglalkozó matematikusok, biológusok és epidemiológusok kompetenciája. Ez egy naiv megközelítés és nem szakértői becslés, ennek ellenére az elemzés kódját nyilvánosan elérhetővé tettem a GITHUB-on, illetve a 17. igazolt hazai beteg megjelenését követő 14. napon megvizsgáljuk a tévedés mértékét egy utánkövető posztban. Reméljük, addigra már a hazai szakemberek professzionális becsléseket is közzétesznek, illetve a kormány határozott intézkedésekkel csökkenti az új-koronavírus-megbetegedés terjedését.
Néhány alapvető információ a COVID-19-ről
- A SARS-CoV-2 burkos RNS vírus.
- Fertőzés: légúti váladékcseppekkel: tüsszentés, köhögés, kilégzés stb.
- Lappangási idő: 2–14 nap (előzetes adat), alap-szaporodási ráta: 2.28 (95% CI 2.06-2.52)
- Tünetek (láz, köhögés, légszomj, felső-légúti tünetek, akut légzőszervi tünetek stb.)
- Tünetek kialakulása esetén, amennyiben járt fertőzött területen, vagy kapcsolatba léphetett fertőzött személlyel, kövesse az NNK utasításait, és keresse telefonon háziorvosát vagy az NNK-t!
Javasolható megelőzési tanácsok
o szabályszerű kézmosás, kézfertőtlenítés
o kontaktus (kézfogás, puszi stb.) kerülése (alternatív üdvözlési módok alkalmazása)
o archoz, szemhez nyúlás teljes kerülése, tárgyak rágásának kerülése
o szellőztetés
o tömegközlekedés, tömegrendezvények, általában a tömeg kerülése
o mobiltelefon-képernyő, készpénz és más potenciálisan “vektorként” működő felületek rendszeres fertőtlenítése vagy használatának kerülése
o fertőzött országok, régiók és személyek kerülése
További információk
(A modellre konstruktív kommenteket a GITHUB oldalra örömmel várok.)