2020. március 11-én készítettem egy naiv becslést a COVID-19 igazolt nyers betegszámának rövid távú hazai alakulására. A vállaltan amatőr (nem vagyok epidemiológus) modellre meglepően sok professzionális, szakmai reflexiót kaptam neves hazai kutatóhelyekről (SE, ELTE, SZTE stb.). Ebben a posztban a március 11-ei becslésem tévedésének mértékéről és főbb okairól írok. A blogposzt végén pedig az OECD-országok előzetesen jelentett adataiból számolt előzetes, nyers halállal végződő megbetegedési arányait (case fatality ratio, CFR) vizualizálom, illetve leírom, hogy ez miért nem a valódi CFR.
Az előző, laikus becslésem tévedésének mértéke
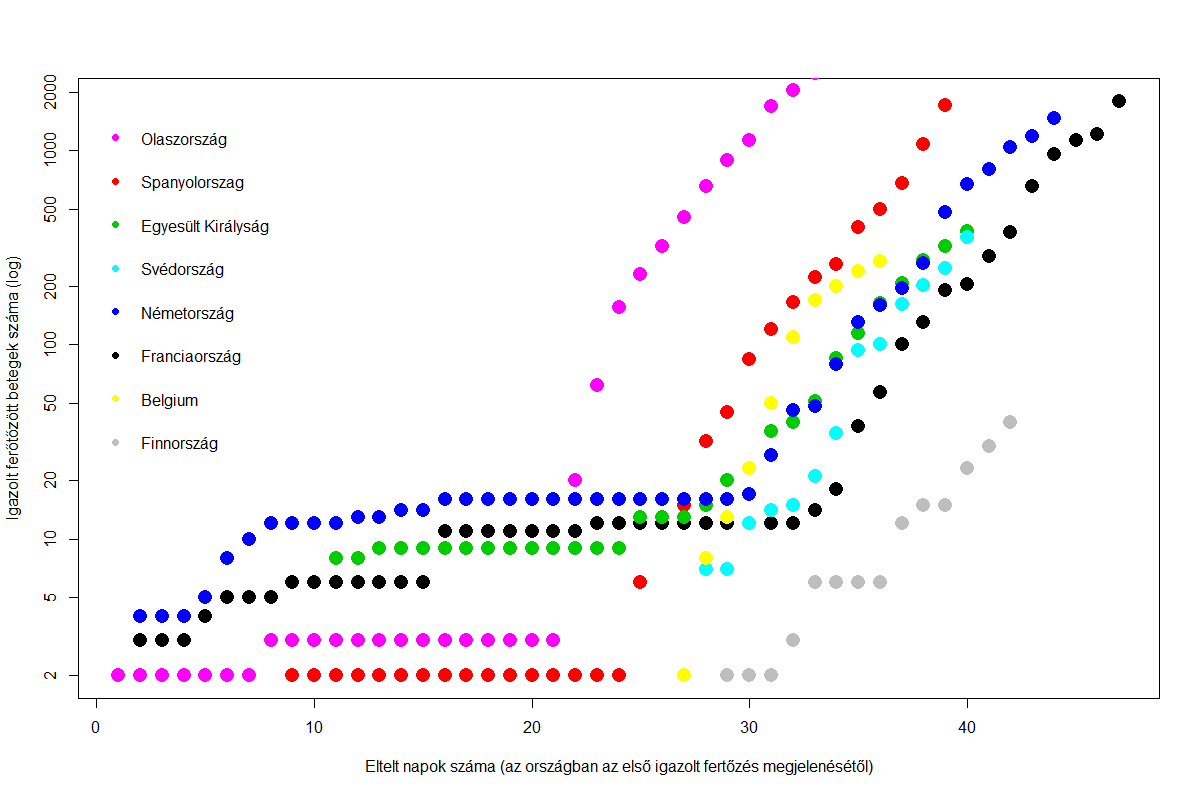
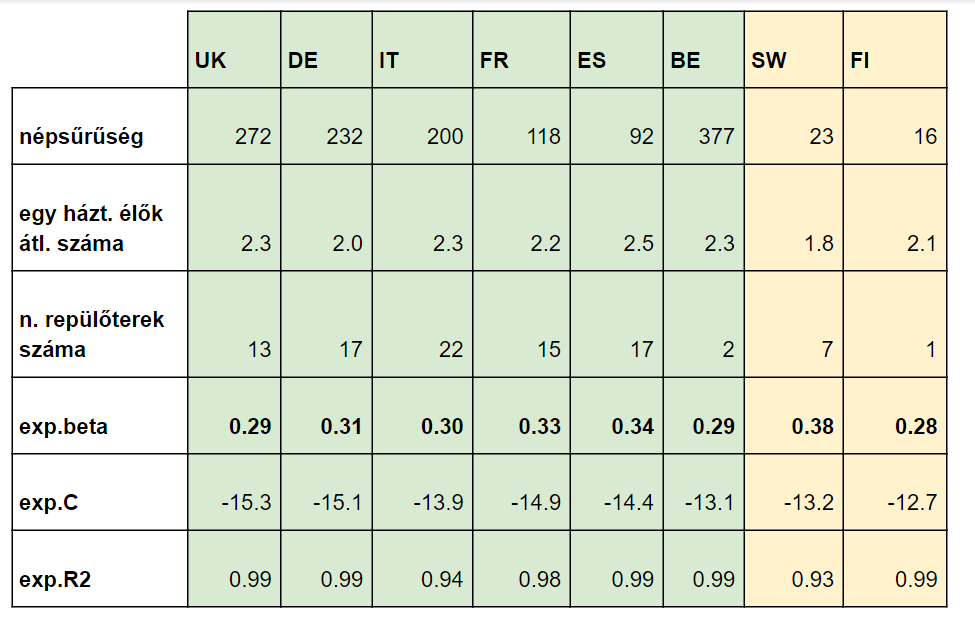
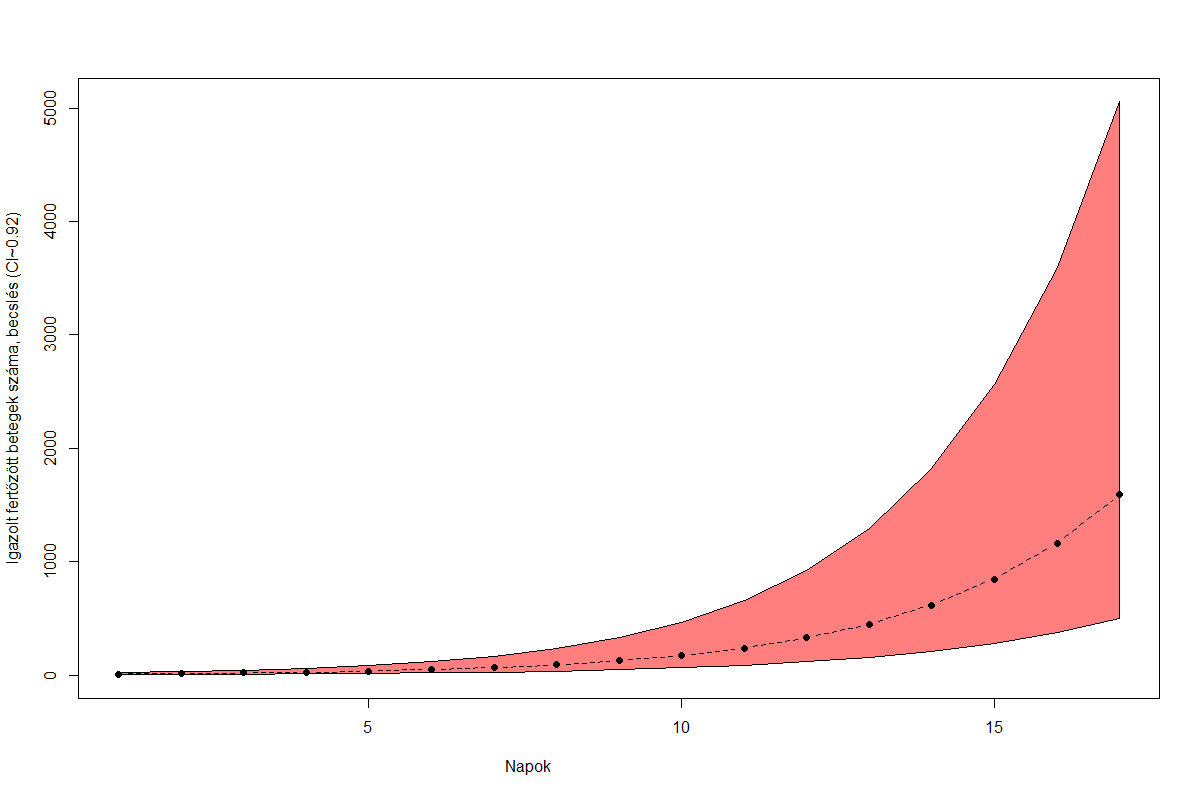
Az március 11-ei becslésben a járvány hazai terjedésének (lakosságarányosan számolva) kezdeti (a 17. igazolt beteg megjelenését követő rövid) szakaszát közelítő exponenciális függvény e kitevőjében lévő szorzóját 0.31 [95% CI 0.29 - 0.34] -re becsültem. A becsléshez nyolc nyugat-európai ország kitevőjét használtam. A hazai valós érték jelenleg alacsonyabb: 0.19 (pseudo R négyzet=0.99). A kitevőben tehát ~35%-ot tévedtem. Ennek megfelelően a jóslásom is pontatlan volt. További bizonytalansági beépítésével azt írtam az előző posztban, hogy „ez a kezdetleges modell a 17. igazolt beteg megjelenése utáni 14. napon 1161 [90% CI 374 - 3599] fertőzöttet jósol”, a valóságban 300 igazolt beteg volt a 17. beteg megjelenését követő 14. napon. Azaz még a tág becslésem alsó határánál (374 igazolt beteg) is 20%-kal kevesebb volt (300). Időben kifejezve 2 napot tévedtem, mert két nap múlva volt 374-nél nagyobb az igazolt fertőzött betegek szám.
Epidemiológus-kutatók felhívták a figyelmem, hogy a becslésem konceptuálisan volt hibás: fejlett országok felfutásából igyekeztem becsülni, de ezen országokban jelentősen más a szűrés rendszere (előfeltételei, módszere, specificitása stb.), illetve az is eltérő, ahogy ezen országok vezetői reagáltak a járványra (relatív időben később és más intézkedésekkel stb.). Szintén más szűrési kapacitással rendelkeztek és a taktikájuk is más volt.
Az igazolt fertőzöttek száma nagy mértékben függ attól, hogy milyen előfeltételek (kockázatok megléte) esetén szűrnek egy országban, ez a feltételrendszer eltolja a mintát, és ez az eltolás minden országban más, emiatt szinte az a meglepő, hogy a tévedésem csak két nap volt.
Az igazolt halálozásoknál pedig az úgynevezett előrehozott halálozás problémája jelenik meg. (Például, ha egy súlyos csontvelőrákos beteg megfertőződik a betegséggel, és meghal, akkor eltérő, hogy melyik ország szűrte előtte és aztán kódolta.) Mindezek miatt csak nagy szaktudással és nagyon korlátozottan hasonlíthatóak össze ezek az előzetesen közölt, nyers adatok. (Egyes statisztikusok szerint tendenciák vizsgálatára sem szabad használni, még egy országon belül sem, illetve ezen duplán torz mintákból súlyos hiba következtetni egy átszűrt lakosság esetében számolható CFR-re.) A COVID-19 járvány valódi halálozási többletéről talán majd akkor mondható valamivel pontosabb állítás, ha a tavalyi regisztrált összes haláleset adatait szakértő epidemiológusok (a megfelelő korrekciókkal) összevetik a jelenlegi hetek halálozási adataival. (De természetesen a halálozási többlet sem fog pontos képet adni, mert azt is áthatja számos tényező, a koráltozó rendelkezések számos ember életmódjára hatottak, változtattak az egészségügyi ellátáson, illetve a légszennyezettségen, mindezeket nagyon nehéz pontosan kiszűrni az adatokból.) Összességében elmondható, hogy most még tendenciákat is nehéz becsülni, mert annyi tényező hatja át a fertőzöttségi és halálozási adatokat. Persze a járvány jóslása érdekében, bizonyos mértékben elkerülhetetlen ennek megkísérlése és néhány kiváló hazai matematikus és orvos-biostatisztikus erre tesz is kísérleteket.
A kutatások tükrében az is látszik, hogy a korfát, a településszerkezetet, a népsűrűséget, az egészségügyi ellátás számos paraméterét, a gazdasági fejlettség mutatóit, a közlekedést, a korlátozásokat és a szálló-por koncentrátumát is figyelembe kell venni. [Bevonható lenne még számos más adatforrás: távközlési, tömegközlekedési, adóügyi (blokkok kiadása), digitális stb. – szinte minden, ami utalhat a vírus terjedésének valószínűsége szempontjából fontos mozgásokra és sűrűsődésére.]
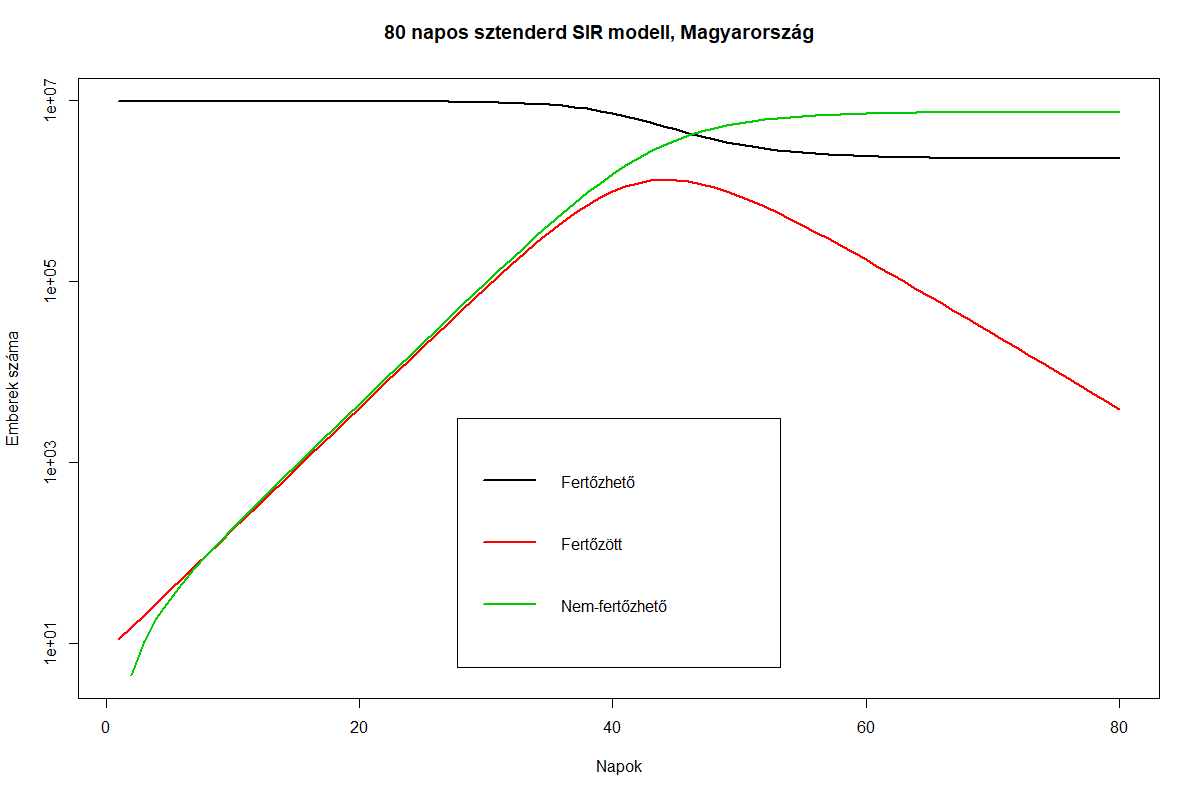
Az első blogposztomban szereplő SIR modell is örökölte a becslés hibáját, és az eredményeimet tovább torzította az átlagtér modellek alapvető korlátja is: az emberek a valóságban nem egyenletesen keverednek, és a különféle csoportok viselkedése is inhomogén. (Persze erre vannak korrekciók, de ezeket az egyszerű modellem nem alkalmazta.)
Az alap szaporodási rátával számoló modellek esetében nehézség, hogy az R0 helyes kiszámítása nagy szakmai odafigyelést és tudást kíván meg, nem csak egy osztást jelent, mint a legtöbb laikus/naiv számításban. Az R0 adatgeometriai szempontból egy többdimenziós valószínűségi tér egy pontját számolja ki, ám az a tér egyik dimenziójában sem normális (illetve Johnson SU családba tartozó) eloszlású. Viszont kiemelhető, hogy kínai kutatók tavaly teljesen új, hálózati értelmezési keretet javasoltak az R0 megközelítésére. Ám Giulio Viceconte and Nicola Petrosillo szerint az R0 nem képes jól megragadni a járványterjedés komplex mechanizmusait. (Fontos jelezni, hogy a sajtóban keveredik néha két fogalom: az alap szaporodási ráta nem azonos a kontagiozitási (fogékonysági) indexszel, amely objektív biológiai mutató, azt mutatja meg, hogy azok közül, akik fertőződtek, hány százalék lesz tényleg fertőzött. Bárányhímlő esetében ez pl. közel 100%.)
Az átlagtér-modelleknél jelentősen pontosabb becslést adó gráffolyamat-modellek megalkotásához viszont sok jó minőségű adatra volna szükség. Ez jelenleg még nem áll rendelkezésre, ezért kénytelenek a kutatók közelítő módszereket alkalmazni, illetve előző járványok már feltárt gráf-folyamataiból következtetni. Az egyik szerintem kifejezetten ígéretes hálózati kaszkád-modell a Generalized Inverse Infection Model, amely a járvány terjedése szempontjából releváns tényezőket a járvány valódi terjedése alapján épített gráfból, élsúlyozás számításával mutatja ki, ez a modell előrejelzésre is alkalmas. Ez a modell még nem került széles körben alkalmazásra, de hazai vonatkozása is van: a modell megalkotói között pedig több ismert szegedi matematikus is van, illetve a – jelenleg Johns Hopkins Egyetemen dolgozó – Lauren Gardner is.
A halálozási arányok
Míg az epidemiológus-kutatók számára a hazai adatok még nem elégségesek pontos halálozási arány (pontosabban: case fatality rate, halállal végződő megbetegedési arány, CFR) becslésére, a laikus sajtó – érthető módon – sokat foglalkozik a kérdéssel, és különféle megállapításokra jut. Habár a fent leírt okok (szűrés rendszerének különbségei, ellátórendszer különbségei, halálozás minősítési rendszer különbségei stb.) miatt a különböző országok előzetesen közölt, nyers arányszámainak alakulását túl sok tényező hatja át, ezért ezekből a valós CFR nem becsülhető pontosan. A valódi CFR tekintében a szakemberek között nincs még egyetértés. 2020. március 30-án a Lancet-ben publikált tanulmány szerint a nyers kínai érték az előzetes halállal végződő megbetegedési arányszáma 2.29% (2.15–2.43), a cenzúrára-korrigált 3.67% (3.56–3.80), a több tényezőre korrigált érték pedig 1.38% (1.23–1.53). Ám a neves stanfordi epidemiológus, John P. A. Ioannidis szerint talán még az elképzelhető, hogy 1% körüli (esetleg alatti) a CFR-érték.
A fent leírt erős korlátok a tudatában mindössze exploratív és nem deskriptív céllal összehasonlítottam, hogy az OECD-országokban milyen tartományban mozog jelenleg – az előzetes gyorsjelentések alapján, az úgynevezett nyers COVID-19 CFR. Hangsúlyoznám, hogy az eltérő szűrési és jelentési protokollok miatt ezek nem hasonlíthatóak közvetlenül össze, tendenciára is nehéz következtetni belőlük, illetve semmiképpen sem a valós CFR értéket mutatják!
A többféle módszer közül a legegyszerűbbet választottam: a Johns Hopkins által a GITHUB-on megosztott adathalmazt használtam a vizualizációhoz. Az adatokat országszintre aggregáltam, majd minden egyes napra jelentett igazolt fertőzött adatokat elosztottam ugyanazon napra jelentett igazolt halálozási adattal. (Ebben az esetben nem alkalmaztam lakosságarányosítást, mert nem változtatott volna az arányon.) Az így kapott országszintű adatoknál kiszámoltam az időben változó arányszám alapparamétereit (vektor hossza, átlag, medián, minimum, maximum, eloszlás tesztelés eredményei stb.).
OECD-országok COVID-19-betegek nyers CFR arányszámai az előzetesen közölt nyers adatok alapján. (Dátum: 2020. április 2. Adatok forrása: Johns Hopkins Egyetem).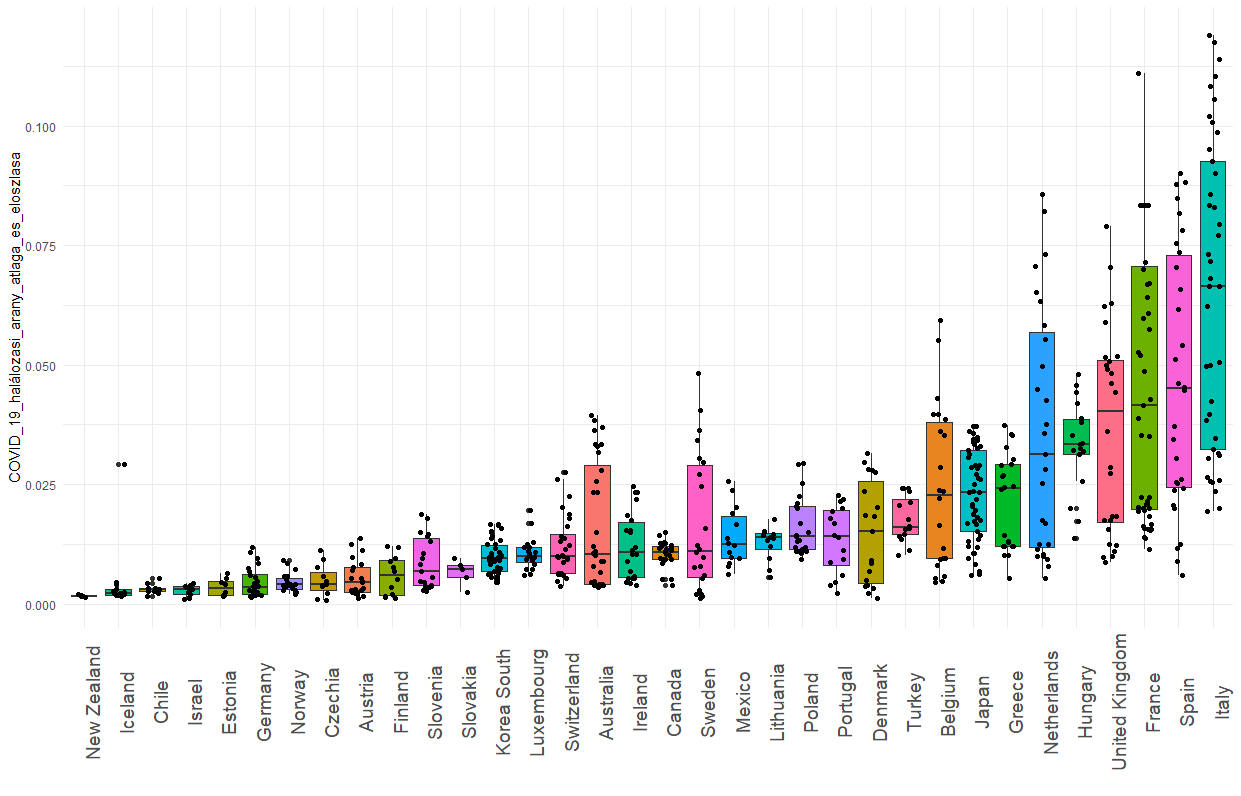
Néhány alapvető információ a COVID-19 megbetegedésről
- A SARS-CoV-2 burkos RNS vírus.
- Fertőzés: elsősorban légúti váladékcseppekkel: tüsszentés, köhögés, kilégzés stb.
- Lappangási idő: 2–14 nap (előzetes adat)
- Tünetek (láz, köhögés, légszomj, felső-légúti tünetek, akut légzőszervi tünetek stb.)
- Tünetek kialakulása esetén, amennyiben járt fertőzött területen, vagy kapcsolatba léphetett fertőzött személlyel, kövesse az NNK utasításait, és keresse telefonon háziorvosát vagy az NNK-t!
Javasolható megelőzési tanácsok
o szabályszerű kézmosás, kézfertőtlenítés
o kontaktus (kézfogás, puszi, ölelés stb.) kerülése (alternatív üdvözlési módok alkalmazása)
o archoz, szemhez nyúlás teljes kerülése, tárgyak rágásának kerülése
o szellőztetés, felületek szakszerű fertőtlenítése
o tömegközlekedés, tömegrendezvények, általában a tömeg kerülése, 2 méteres távolság tartása
o mobiltelefon-képernyő, készpénz, állatok és más potenciálisan “vektorként” működő felületek rendszeres fertőtlenítése vagy használatának kerülése
o fertőzött országok, régiók és személyek kerülése, (sebészeti) maszk használata
o különösen fontos az idősek és az immunrendszert érintő betegségekben szenvedők védelme!
o kormányzati, hatósági és az orvosi kérések maradéktalan betartása!
További információk
Nemzeti Népegészségügyi Központ
SE Rektori tájékoztató
https://koronavirus.gov.hu/
Habár ez nem tudományos igényű munka, hanem csak egy egyszerű exploratív vizualizáció, mégis az R-ben készült program kódját felraktam GITHUB-ra, megjegyzéseket, javítási ötleteket szintén a GITHUB-ra várok.